Chi-square Analysis in a Research
Theory of analysing categorical data
-
-
- Simplest case: analysing 2 categorical variables.
- To investigate the relationship between categorical variables.
-
– We cannot use the mean because we the data are not continuous measurements.
– So we analyse frequencies.
CHi-Square
-
-
- When do you use a Chi-square test? The purpose of a Chi-square test is to compare the observed distribution of numbers in certain categories with a hypothesised distribution of data.
- It is appropriate to use when:
-
– The sampling method is simple random sampling,
– The population is more than 10 times larger than the sample
– The variable under study is categorical and each level of the categorical variable has an expected frequency count of at least 5.
-
-
- This test allows us to compare a collection of categorical data with some theoretical expected distribution.
-
Pearson’s Chi-square test
-
-
- This according to Andy Field is an extremely elegant statistic based on comparing the frequencies that occur in those categories compared to what you would expect in those categories by chance.
- Previously we looked at deviation = Σ (observed – model) 2
-

Procedure
-
-
- First we must check that we are not violating any assumptions of the Chi-square test. Our data may not be valid if we have a small sample size.
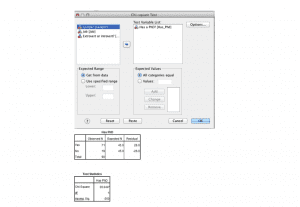
- Each cell must contain at least 5 data. If the smallest number is greater than 5 then use SPSS to calculate the Chi-square statistics.
-
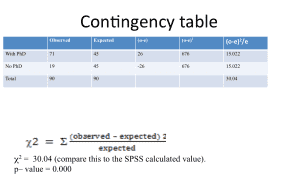
- Calculate the chi-square statistic x2 by completing the following steps:
- For each observed number in the table subtract the corresponding expected number (o— e).
- Square the difference [ (o —e)2 ].
- Divide the squares obtained for each cell in the table by the expected number for that cell [ (o – e)2 / e ].
- Sum all the values for (o – e)2 / e. This is the chi-square statistics.
-
For our example the contingency table for this is:
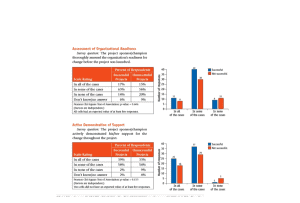
If you like this article, see others like it: